이번엔 Normal Mapping을 추가해보았다.
Normal Mapping이란, 버텍스를 늘리지 않으면서 표면의 복잡성을 취하는 기술이다.
생각해보면, 우리가 처음 텍스쳐를 쓴 이유도 물체 표면의 컬러의 복잡함을 구현하기 위해 버텍스를 여러개 쓰기보다는, 그걸 텍스쳐라는 독립적인 자료구조에 저장하기 위한 것이었다.
Normal Map도 이와 똑같다. 다만, 텍스쳐라는 자료구조에 저장하는 것이 컬러 정보가 아닌 normal 정보인 것이다.

Normal Mapping의 가장 대표적인 예시이다.
고전적인 방식대로 우측의 결과물을 구현하고자 한다면, 벽돌이 들어가고 나오는 부분마다 버텍스를 포지션을 달리해서 왕창 심어줘야 했겠지만, normal map의 사용을 통해 기존과 마찬가지로 버텍스 4개만 사용하고도 저렇게 현실적인 라이팅을 구현할 수 있는 것이다.

그런데 normal mapping을 사용할 때 상기해야할 점이 있는데, 물체는 월드에 회전되어 놓여질 수 있다는 점이다.
모든 normal map들은 기본적으로 그 텍스쳐가 붙는 표면이 +z축을 바라본다고 가정하고 만들어져있다.
즉 xy 평면 위에 반듯하게 놓여져 있다고 가정되어있는 것이다.
이 때문에 물체의 표면이 +z축을 바라보지 않도록 회전하는 순간, 라이팅이 이상해진다.

이를 해결하기 위해서 Tangent Space라는 또 하나의 좌표계를 정의할 것이다.
Tangent Space는 폴리곤의 표면을 기준점으로 하는 좌표계이다.
표면이 향하는 쪽을 +Z축으로 간주한다. 즉, normal map이 따르는 좌표계라고 할 수 있다.
그리고 Tangent Space에서 World Space로의 변환 행렬을 TBN 행렬이라고 한다.
따라서, 우리는 normal map에서 Tangent Space 기준 normal을 읽어, 그것을 TBN 행렬로 변환하여 World Space 기준 normal을 얻어낼 수 있다.
TBN이라는 이름은 Tangent, Bitangent, Normal에서 하나씩 따온 것이다.
Tangent, Bitangent, Normal은 각각 3차원 벡터이다.
행렬의 구조는 다음과 같다.

행렬이 왜 이렇게 생겼는지는 곧 바로 후술할 것이다.
각 벡터는 어떠한 surface에서 다음과 같이 정의된다.

N(ormal) 벡터는 텍스쳐가 칠해지는 표면이 향하는 방향이고,
T(angent)와 B(itangent) 벡터는 각각 텍스쳐 좌표계의 x, y축을 의미함을 알 수 있다.
다시 위의 행렬이 왜 저렇게 만들어졌는지 생각해보자면,
T, B, N은 Tangent Space의 기저 벡터(basis vector)라고 할 수 있다.
그에 따라 물론 T, B, N은 단위벡터이다.
즉 유클리드 좌표계로 따지면 x, y, z축에 해당하는 것이고,
유클리드 좌표계를 사용하는 World Space에서 TBN 좌표계를 사용하는 Tangent Space로의 변환 행렬은 다음과 같다.
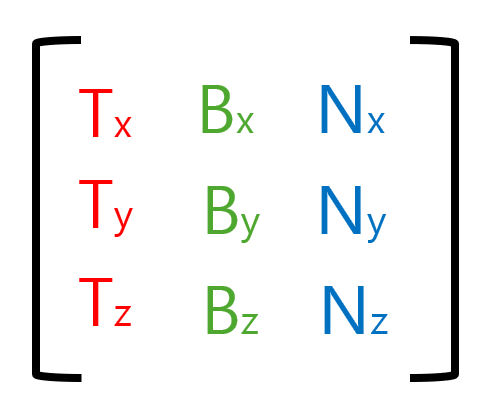
이는 좌표계를 바꾸는 Change of basis 행렬이다.
즉 1, 2, 3열이 각각 새로운 x축, y축, z축을 의미한다.
그런데 우리가 원하는 변환은 World Space에서 Tangent Space로의 변환이 아니고,
Tangent Space에서 World Space로의 변환이다.
따라서 TBN 행렬은 위의 저 행렬의 역행렬과 같다.
그런데, 이렇게 3개의 축이 서로 직교할 때(직교행렬), 역행렬은 전치행렬과 같다.
그 이유는 https://ciel45.tistory.com/91 여기에서 다룬 적 있는데, 한번 더 상기해보자면
TBN과 TBN의 역행렬을 곱하면 단위행렬이 나와야 하는데,
각 벡터가 모두 직교하므로 두 벡터의 곱이 1이 나오기 위해서는 서로 같은 벡터끼리 곱해져야한다.
직교하는 두 벡터의 내적값은 0이 되어버리기 때문.
그래서 행렬의 곱셈의 과정을 고려했을 때, 결과물의 대각 성분에 T끼리, B끼리, N끼리 곱한 값이 들어갈 수 있도록 하려면 곱해지는 것이 TBN의 전치행렬이어야 한다. 즉 역행렬이 곧 전치행렬이 된다.
그래서 TBN 행렬이 이렇게 생긴 것이다.
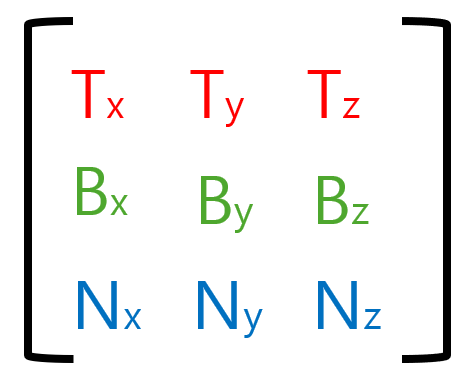
그럼 이제 우리가 N은 알고 있으니(표면의 normal 벡터), tangent와 bitangent 벡터를 계산해야 한다.
이를 계산하는데는 텍스쳐 좌표를 사용하게 된다.

이 normal map을 써서 그려질 폴리곤이 저 삼각형이라고 생각하면,
우리는 버텍스마다 텍스쳐 좌표를 알고 있으므로 위 그림의 U1, V1, U2, ...는 다 알고있다.
이를 통해 델타U1, 델타V1, 델타U2, 델타V2를 구할 수 있다.
그러면 삼각형의 엣지 E1, E2를 T와 B에 대한 식으로 나타낼 수 있다.
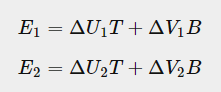
여기에서 E, T, B를 3차원 벡터로 풀어 쓰면 다음과 같다.
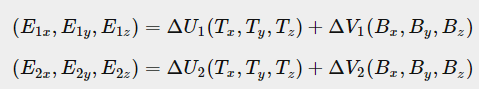
여기서 델타 값들은 다 텍스쳐 좌표로 구해놓은 것이고, E값 역시 버텍스 포지션끼리의 차를 이용하여 구할 수 있다.
우리가 저 식에서 모르는 것은 T, B뿐이다.
식을 행렬을 이용해 예쁘게 정리하면 다음과 같다.

여기서 우항에 T, B만 남기기 위해, 양변에 저 델타행렬의 역행렬을 곱하면 다음과 같다.
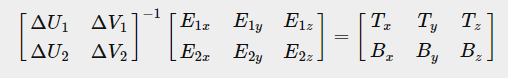
그럼 이제 좌항을 쭉 계산해주면 끝이다. 2x2 역행렬은 우리에게 익숙한 ad-bc 뭐시기 그 공식 써주면 된다.
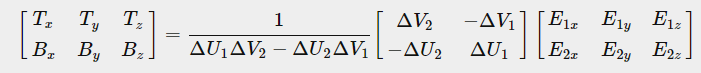
이렇게 tangent, bitangent 벡터를 구할 수 있다.
그런데.. 사실 실제로는 이렇게 직접 계산할 필요 없이 assimp에서 이걸 다 계산해준다.
void Model::LoadModel(const std::string& fileName)
{
//...
Assimp::Importer importer;
const aiScene* scene = importer.ReadFile("Models/" + fileName,
aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_GenSmoothNormals | aiProcess_JoinIdenticalVertices |
aiProcess_CalcTangentSpace);
//...
}
aiProcess_CalcTangentSpace 옵션을 주면 버텍스마다 Tangent, Bitangent 벡터가 뿅 생긴다.
이렇게 생긴 벡터들은 aiMesh->mTangents, aiMesh->mBitangents에서 가져다 쓰면 된다.
void Model::LoadMesh(aiMesh* mesh, const aiScene* scene)
{
std::vector<Vertex> vertices;
//...
// vertices 채워주기
for (size_t i = 0; i < mesh->mNumVertices; i++)
{
Vertex vertex;
InitVertexBoneData(vertex);
//...
// tangent, bitangent
vertex.Tangent = AssimpGLMHelpers::GetGLMVec(mesh->mTangents[i]);
vertex.Bitangent = AssimpGLMHelpers::GetGLMVec(mesh->mBitangents[i]);
vertices.push_back(vertex);
}
//...
}
void Mesh::CreateMesh(std::vector<Vertex>& vertices, std::vector<unsigned int>& indices, std::string name)
{
//...
// tangent
glVertexAttribPointer(3, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)(offsetof(Vertex, Tangent)));
glEnableVertexAttribArray(2);
// bitangent
glVertexAttribPointer(4, 3, GL_FLOAT, GL_FALSE, sizeof(Vertex), (void*)(offsetof(Vertex, Bitangent)));
glEnableVertexAttribArray(2);
//...
}
이렇게 GPU로 쏴줬다면, Vertex Shader 코드는 다음과 같다.
// vertex.glsl
#version 330
//...
layout (location = 2) in vec3 normal;
layout (location = 3) in vec3 tangent;
layout (location = 4) in vec3 bitangent;
//...
//...
out mat3 TBN;
uniform mat4 modelMat;
uniform mat4 PVM;
uniform mat3 normalMat;
void main()
{
//...
vec3 T = normalize(normalMat * tangent);
vec3 B = normalize(normalMat * bitangent);
vec3 N = normalize(normalMat * normal);
TBN = mat3(T, B, N);
}일단 T,B,N 벡터들이 쓰는 좌표계를 바꿔준다.
CPU에서 T, B, N을 계산할 때 버텍스의 포지션을 그대로 사용했으므로, 처음엔 Model Space에 존재한다.
여기에 Normal Matrix를 곱해줌으로써 World Space로 바꿔준다.
Normal Matrix에 대한 자세한 설명은 https://ciel45.tistory.com/102
[OpenGL] Normal Transformation (Normal Matrix)
학교 컴퓨터 그래픽스 수업에서는 적당히 언급만 하고 넘어갔던 부분이라서, 개인적으로 공부해보았다. Phong Reflection Model을 통한 쉐이딩을 위해서는 물체의 표면의 normal을 구해야 한다.이 때
ciel45.tistory.com
이제 Fragment Shader에서는 TBN 행렬을 이용해 normal을 Tangent Space에서 World Space로 바꿔줄 것이다.
// fragment.glsl
#version 330
//...
in mat3 TBN;
out vec4 FragColor;
//...
uniform sampler2D colorSampler;
uniform sampler2D normalSampler;
//...
//...
void main()
{
vec4 texColor = texture(colorSampler, TexCoord);
vec3 texNormal = texture(normalSampler, TexCoord).rgb; // normal map에서 떼어오기
texNormal = texNormal * 2.0 - 1.0; // 값의 범위를 [0,1]에서 [-1,1]로 remap
texNormal = normalize(TBN * texNormal);
vec4 finalColor = vec4(0,0,0,0);
finalColor += CalcDirectionalLight(texNormal);
finalColor += CalcPointLights(texNormal);
FragColor = texColor * finalColor;
}main 함수 내부 line 2~4를 보면 된다.
이외에 CPU 쪽에서 normal map을 로드하고, GPU에 쏴주고하는 것은 그냥 여타 텍스쳐를 불러오는 과정이랑 똑같아, 굳이 다시 쓰진 않으려고 한다.
[OpenGL] Textures (4) - 로드(stb_image), 생성, 바인딩(Texture Unit)
이번엔 코딩을 통해 실제로 텍스쳐를 입혀볼 것이다. 먼저 디스크에 저장된 이미지 파일을 메인 메모리에 로드해야하는데, 처음이면서도 가장 어려운 부분이다.다행히도 이걸 손쉽게 할 수 있
ciel45.tistory.com
결과 (좌 : 적용 전, 우 : 적용 후):
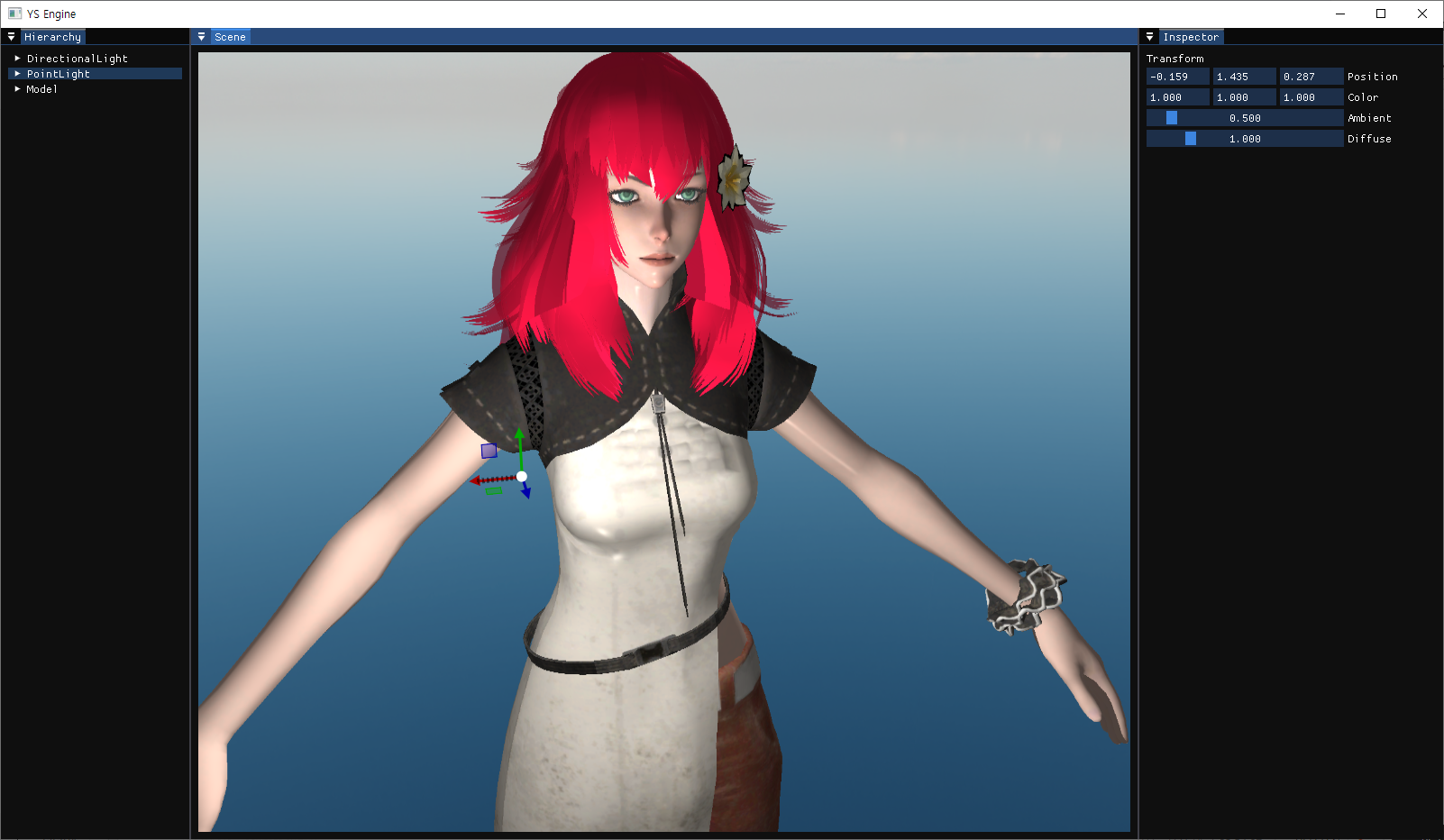





확실히 옷의 주름 등의 표현이 더욱 디테일해진 것을 볼 수 있다.
'OpenGL > 개발 일지' 카테고리의 다른 글
| [OpenGL] 게임 엔진 개발 (9) - 플레이어 이동 (1) | 2024.08.20 |
|---|---|
| [OpenGL] 게임 엔진 개발 (8) - Terrain (0) | 2024.08.12 |
| [OpenGL] 게임 엔진 개발 (6) - Scene Hierarchy (0) | 2024.07.30 |
| [OpenGL] 게임 엔진 개발 (5) - Skeletal Animation (3) (0) | 2024.07.26 |
| [OpenGL] 게임 엔진 개발 (4) - Skeletal Animation (2) (0) | 2024.07.26 |